Turing Reductions
October 13, 2025
Learning objectives
Learning Objectives for Theoretical Machines
- CS-204-1: Use both intuitive analysis and theoretical proof techniques to correctly distinguish between problems that are tractable, intractable, and uncomputable.
- CS-204-2: Correctly use one or more variants of the Turing machine (TM) abstraction to both describe and analyze the solution to a computational problem.
- CS-204-3: Correctly use one or more variants of the finite state machine (FSM) abstraction to describe and analyze the solution to a computational problem.
- CS-204-4: Use a formal proof technique to correctly classify a problem according to whether or not it is in the P, NP, NP-Hard, and/or NP-Complete complexity class(es).
- CS-204-5: Apply insights from theoretical proofs concerning the limits of either program feasibility or complexity to the implementation of both correct and efficient real-world Python programs.
Reduction techniques, like Turing reduction, aid when proving that a problem is “hard”!
- “Reduction for hardness” helps with learning objective CS-204-4, in which you learn how to prove a problem is uncomputable or otherwise “hard”. Okay, let’s dive in!
Prove computational problem is hard
Main goal: Prove a problem is uncomputable - We suspect a problem cannot be solved by any algorithm
- Need rigorous mathematical proof to establish this fact
- Cannot just say “it seems hard” or “I can’t think of a solution”
Two proof approaches to try: - Contradiction: As before, prove uncomputability by contradiction
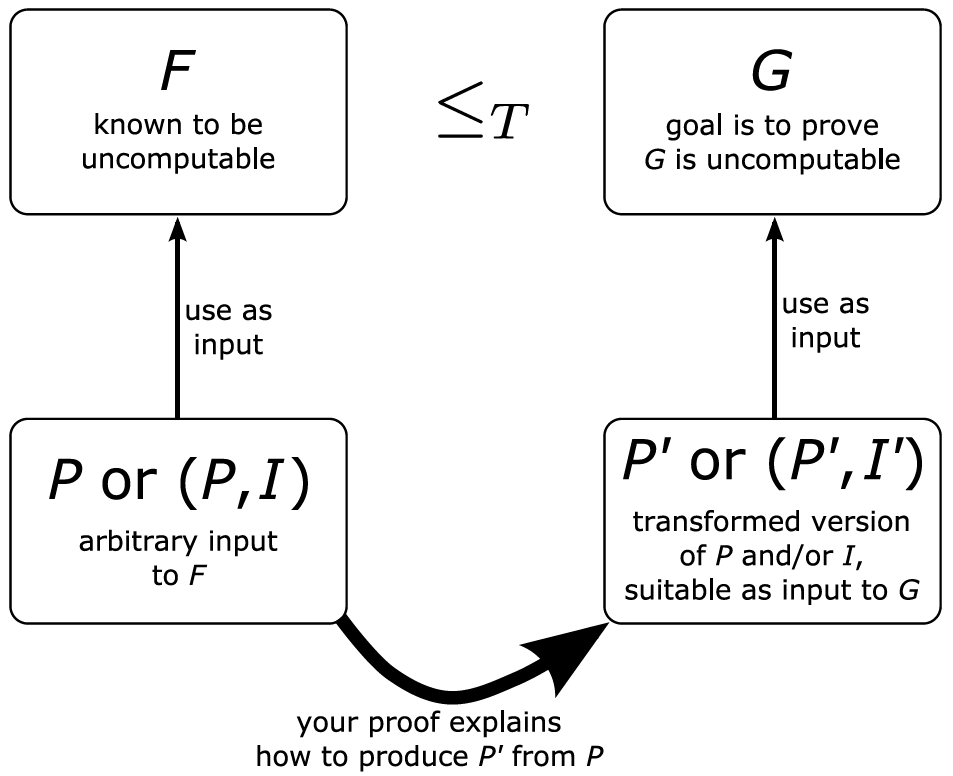
- Reduction: Constructively transform a known uncomputable problem \(F\) to a new problem \(G\), thereby showing that problem \(F\) is “no harder than” new problem \(G\) and that \(G\) is also uncomputable
- Let’s explore reduction proofs for problem uncomputability!
Why do reductions work?
- We have a problem \(F\) that is already proven to be uncomputable
- We want to prove a new problem \(G\) is also uncomputable — without having to “start from scratch” for this proof for \(G\)’s uncomputability!
- Reduction from \(F\) to \(G\) means we can solve \(F\) using a solution for \(G\)
Steps: Still proceed by contradiction to prove reduction works: - Assume \(G\) is computable
- Construct a reduction from \(F\) to \(G\)
- This means that \(F\) is also computable
- This contradicts the fact that \(F\) is uncomputable
- This means the initial assumption was incorrect
- We can therefore conclude that \(G\) is uncomputable
Example of “reduction” concepts

Reduction concept as Python function
import utils; from utils import rf
from lastDigitIsEven import lastDigitIsEven
def isOddViaReduction(inString):
inStringPlusOne = int(inString) + 1
return lastDigitIsEven(str(inStringPlusOne))
def testisOddViaReduction():
testVals = [('-2', 'no'),
('0', 'no'),
('2', 'no'),
('3742788', 'no'),
('-1', 'yes'),
('1', 'yes'),
('3', 'yes'),
('17', 'yes'),
('3953969', 'yes'),
]
for (inString, solution) in testVals:
val = isOddViaReduction(inString)
utils.tprint(inString, ':', val)
assert val == solutionisOddViaReductionuseslastDigitIsEvento solve theisOddproblemisOddViaReductionsolvesisOddby “reducing” it tolastDigitIsEven
Define the lastDigitIsEven function
import utils; from utils import rf
def lastDigitIsEven(inString):
lastDigit = inString[-1] # ``[-1]'' is Python notation for last element
if lastDigit in '02468':
return 'yes'
else:
return 'no'
def testlastDigitIsEven():
testVals = [('-2', 'yes'),
('0', 'yes'),
('2', 'yes'),
('3742788', 'yes'),
('-1', 'no'),
('1', 'no'),
('3', 'no'),
('17', 'no'),
('3953969', 'no'),
]
for (inString, solution) in testVals:
val = lastDigitIsEven(inString)
utils.tprint(inString, ':', val)
assert val == solution- This
lastDigitIsEvenfunction can solve theisOddproblem - The
isOddViaReductionbehaves the same way as theisOddfunction
What is a Turing reduction?
Formal definition: - Let \(F\) and \(G\) be computational problems
- \(F\) has a Turing reduction to \(G\) if we can solve \(F\) using a program for \(G\)
- We write this as \(F \leq_T G\) (read this notation as “\(F\) reduces to \(G\)”)
Intuitive meanings: - “\(F\) is easier than \(G\)” or “\(F\) is no harder than \(G\)”
- If \(G\) is computable, then \(F\) is automatically computable
- If \(F\) is uncomputable, then \(G\) must also be uncomputable
- Visually, write the notation \(F \leq_T G\) as \(F \rightarrow G\) in a diagram
Prove uncomputability using Turing reductions
- Explore the properties of Turing reductions
- By reducing from
YesOnString:- Prove that
ContainsGAGAis uncomputable - Prove that
HaltsOnStringis uncomputable - Importantly, many other reductions are also possible!
- Done correctly, a reduction proves uncomputability
- Prove that
- Visualize a tree of uncomputable problems and their relationships
YesOnString \(\rightarrow\) ContainsGAGA
Goal: Prove ContainsGAGAis uncomputableKnown fact: YesOnStringis uncomputableStrategy: Show YesOnString\(\leq_T\)ContainsGAGA
Problem definitions: YesOnString: Given program \(P\) and input \(I\), does \(P(I)=\) “yes”?ContainsGAGA: Given program \(P\) and input \(I\), does \(P(I)\) contain the string “GAGA”?
Reduction strategy: - Transform any instance of
YesOnStringinto an instance ofContainsGAGA(i.e.,ContainsGAGAwill computeYesOnString) - Use “oracle” for
ContainsGAGAto solve theYesOnStringproblem
- Transform any instance of
Define the yesViaGAGA program
import utils; from utils import rf
from GAGAOnString import GAGAOnString # oracle function
def yesViaGAGA(progString, inString):
singleString = utils.ESS(progString, inString)
return GAGAOnString(rf('alterYesToGAGA.py'), singleString)
def testYesViaGAGA():
testvals = [
('containsGAGA.py', 'TTTTGAGATT', 'yes'),
('containsGAGA.py', 'TTTTGAGTT', 'no'),
('isEmpty.py', '', 'yes'),
('isEmpty.py', 'x', 'no'),
]
for (filename, inString, solution) in testvals:
val = yesViaGAGA(rf(filename), inString)
utils.tprint(filename + ":", val)
assert val == solutionKey idea: Solve the YesOnStringproblem using an “oracle” forContainsGAGA, meaning we will solve known problem with new one
Define the GAGAOnString program
import utils; from utils import rf
from universal import universal
def GAGAOnString(progString, inString):
val = universal(progString, inString)
if val == 'GAGA':
return 'yes'
else:
return 'no'
def testGAGAOnString():
testvals = [('containsGAGA.py', 'GAGAGAGAG', 'no'),
('repeatCAorGA.py', 'CA', 'no'),
('repeatCAorGA.py', 'GA', 'yes') ]
for (progName, inString, solution) in testvals:
val = GAGAOnString(rf(progName), inString)
utils.tprint( (progName, inString), ":", val )
assert val == solutionKey idea: The GAGAOnStringfunction transforms the output of any program to “yes” if standard output equals “GAGA” or “no” otherwise
Define the alterYesToGAGA program
import utils; from utils import rf
from universal import universal
def alterYesToGAGA(inString):
(progString, newInString) = utils.DESS(inString)
val = universal(progString, newInString)
if val == 'yes':
return 'GAGA'
else:
return 'no'
def testAlterYesToGAGA():
for (progName, inString, solution) in [('containsGAGA.py', 'GAGAGAGAG', 'GAGA'),
('containsGAGA.py', 'ATATACCC', 'no') ]:
progString = rf(progName)
combinedString = utils.ESS(progString, inString)
val = alterYesToGAGA(combinedString)
utils.tprint( (progName, inString), ":", val )
assert val == solutionKey idea: The alterYesToGAGAfunction transforms the output of any program to either “GAGA” if output is “yes” or “no” otherwise
YesOnString \(\leq_T\) ContainsGAGA
yesViaGAGA: uses theGAGAOnString(i.e.,ContainsGAGA) oracle to decideYesOnStringby calling the oracle on the transformed program.yesViaGAGAis functionally equivalent toYesOnString- However,
yesViaGAGAusesGAGAOnStringas a key building block
alterYesToGAGA.py: transforms an instance(P, I)so that ifP(I)returns"yes"the transformed program prints"GAGA", otherwise prints"no".GAGAOnString: oracle wrapper that simulates a program and returns"yes"iff the program’s standard output equalsGAGA.Key insights about this proof technique using Turing reductions:
- Not a “direct” proof by contradiction for
ContainsGAGA’s uncomputability - Instead, we prove
YesOnString\(\leq_T\) (“reduces to”)ContainsGAGA - This reduction means that
YesOnStringis no harder thanContainsGAGA
- Not a “direct” proof by contradiction for
Why does this prove that ContainsGAGA is uncomputable?
Step 1: Assume ContainsGAGAis computableStep 2: Then YesOnStringis computable, via the reductionStep 3: But YesOnStringis uncomputable, which we have previously proven in a separate proof by contradiction!
- Contradiction: Cannot have both computable and uncomputable
- Realization: Our initial assumption about
ContainsGAGAwas wrong - Conclusion:
ContainsGAGAmust be uncomputable via reduction - This completes the proof that
ContainsGAGAis uncomputable!
Tree of uncomputable problems
Starting point: YesOnString, previously proven uncomputableFirst level reductions: Reduce to: YesOnEmpty(does \(P(\epsilon)=\) “yes”?)Reduce to: YesOnAll(does \(P(I)=\) “yes” for all \(I\)?)Reduce to: YesOnSome(does \(P(I)=\) “yes” for some \(I\)?)Reduce to: ContainsGAGA(does \(P(I)\) output contain “GAGA”?)
Second level reductions: From halting: HaltsOnString,HaltsOnEmpty,HaltsOnAllFrom counting: NumCharsOnString,NumStepsOnString
Next question: What are the properties of Turing reductions? And, finally, how can we visualize a tree of reductions?
Properties of Turing reductions
- Transitivity property:
Chain reductions: If \(F \leq_T G\) and \(G \leq_T H\), then \(F \leq_T H\) Composition: Solve \(F\) using \(G\) oracle, solve \(G\) using \(H\) oracle Combined: Can solve \(F\) using \(H\) oracle directly
Key: Importantly, all of these uncomputability proofs start from a single problem, such as
YesOnString, that we’ve proven to be uncomputable!Building hierarchies: Transitivity helps organize problems by hardness
Viewing hierarchies: See the relationships between problems in a tree
Tree Interpretation: Node at the top is the “starting point” of the Turing reduction chain! Okay, let’s see what this uncomputability tree looks like!
Visualize uncomputability tree
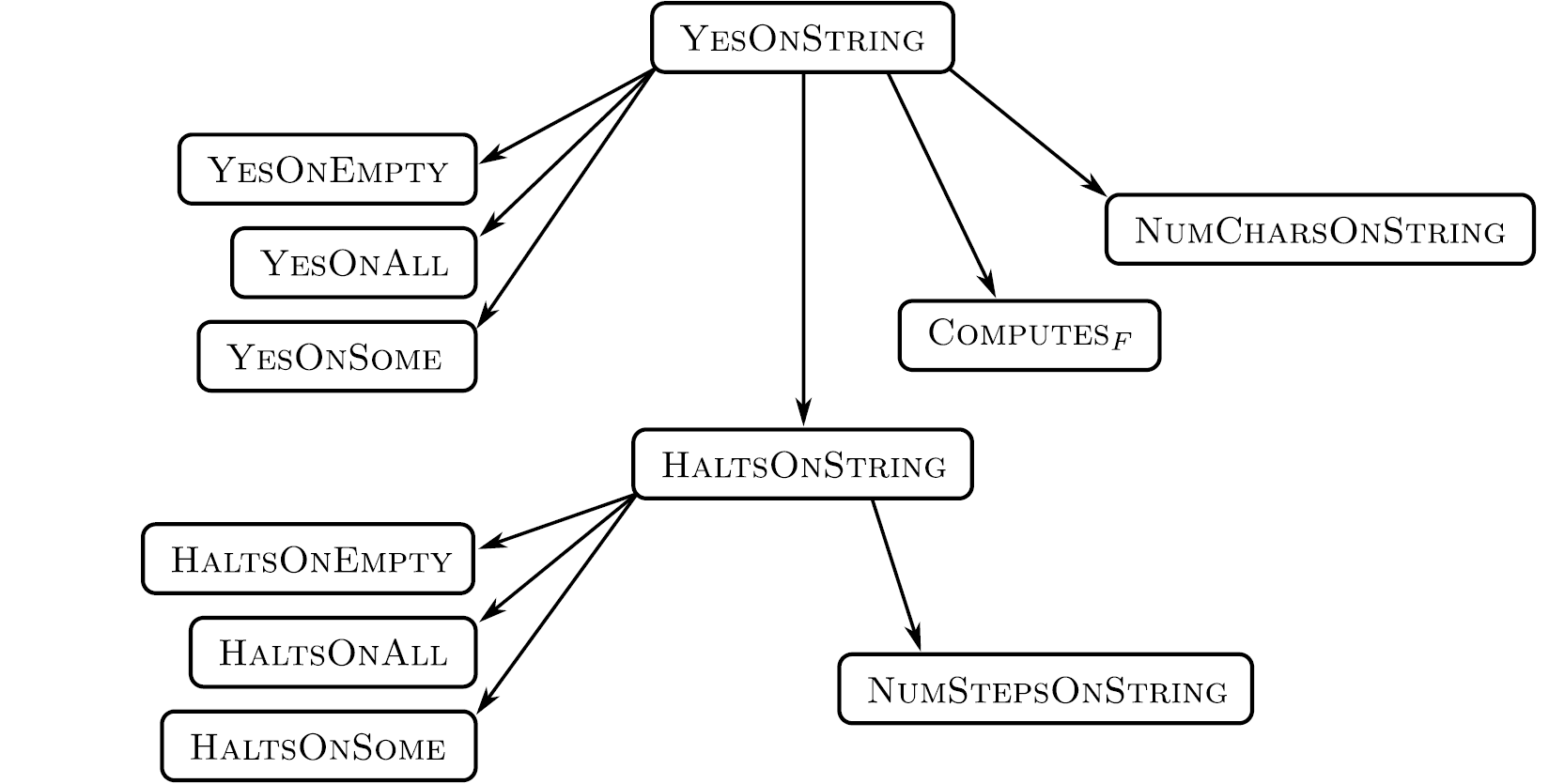
What are different ways that you can express the tree’s relationships?
YesOnStringis no harder thanHaltsOnStringHaltsOnStringis no harder thanHaltsOnEmptyHaltsOnStringis no harder thanNumStepsOnStringYesOnStringis no harder thanHaltsOnEmptyYesOnStringis no harder thanNumStepsOnString
Implications of transitivity
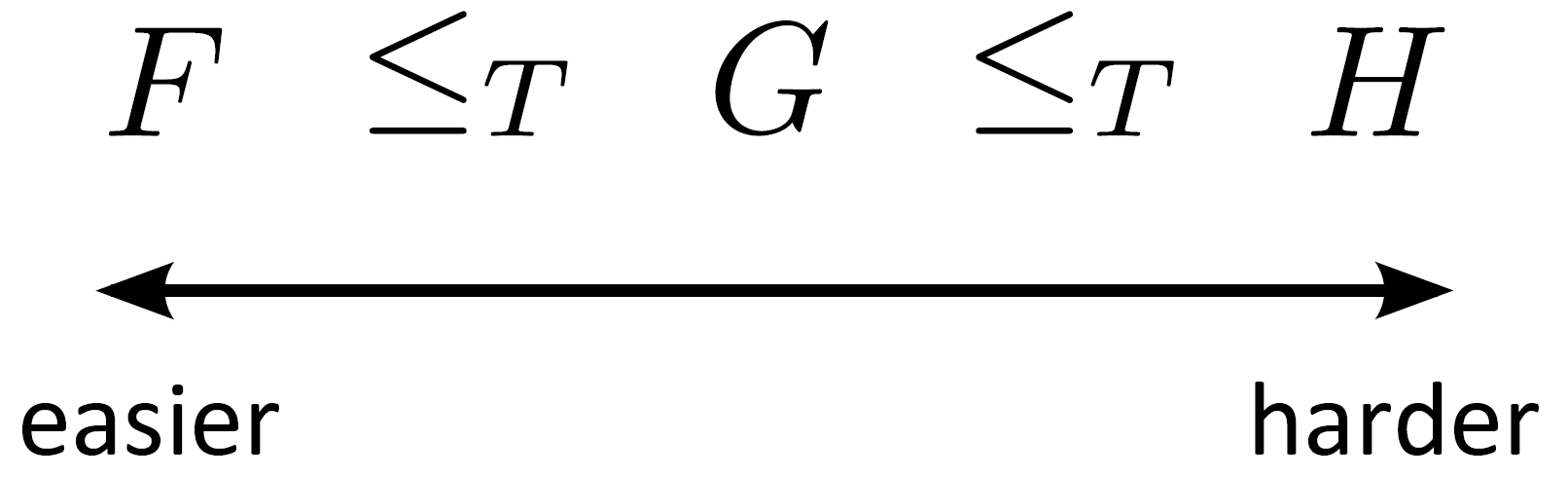
- To start, problem \(F\) is no harder than problem \(G\)
- It also true that problem \(G\) is no harder than problem \(H\)
- By transitivity, problem \(F\) is no harder than problem \(H\)
- The Turing reduction operator \(\leq_T\) orders problems in “increasing levels of hardness” from left (“easier” problems) to right (“harder” problems)
YesOnString to YesOnEmpty
import utils; from utils import rf
from yesOnEmpty import yesOnEmpty # oracle function
def yesViaEmpty(progString, inString):
utils.writeFile('progString.txt', progString)
utils.writeFile('inString.txt', inString)
return yesOnEmpty(rf('ignoreInput.py')) - Use the “ignore input” technique to transform the problem
- Ignoring input helps to create the correct reduction:
YesOnString\(\leq_T\)YesOnEmptyYesOnStringis no harder thanYesOnEmpty- This approach shows that
YesOnEmptyis undecidable
Can we prove that HaltsOnStringis undecidable?
Create yesViaHalt program
import utils; from utils import rf
from haltsOnString import haltsOnString # oracle function
def yesViaHalts(progString, inString):
singleStr = utils.ESS(progString, inString)
return haltsOnString(rf('alterYesToHalt.py'), singleStr)
def testYesViaHalts():
testvals = [
('containsGAGA.py', 'TTTTGAGATT', 'yes'),
('containsGAGA.py', 'TTTTGAGTT', 'no'),
('isEmpty.py', '', 'yes'),
('isEmpty.py', 'x', 'no'),
]
for (filename, inString, solution) in testvals:
val = yesViaHalts(rf(filename), inString)
utils.tprint(filename + ":", val)
assert val == solution- Use the
haltsOnString“oracle” to solveYesOnString, meaningYesOnString\(\leq_T\)HaltsOnString. Next, what is the implementation ofhaltsOnString?
Define the haltsOnString program
import utils; from utils import rf
from universal import universal
def haltsOnString(progString, inString):
# if it doesn't complete before timing out, assume it is in an infinite loop
# note that this is for demonstration purposes only and not how an
# actual "haltsOnString" oracle would be implemented in the proof
val = utils.runWithTimeout(None, universal, progString, inString)
if val != None:
return 'yes'
else:
return 'no'
def testhaltsOnString():
for (progName, inString, solution) in [
('loopIfContainsGAGA.py', 'GAGAGAGAG', 'no'), \
('loopIfContainsGAGA.py', 'TTTTGGCCGGT', 'yes') ]:
val = haltsOnString(rf(progName), inString)
utils.tprint( (progName, inString), ":", val )
assert val == solution- This approximate version uses
runWithTimeoutto simulate halting behavior since theuniversalprogram may run forever with programs having infinite loops
Define the alterYesToHalt program
import utils; from utils import rf
from universal import universal
def alterYesToHalt(inString):
(progString, newInString) = utils.DESS(inString)
val = universal(progString, newInString)
if val == 'yes':
# return value is irrelevant, since returning any string halts
return 'halted'
else:
# deliberately enter infinite loop
utils.loop()
def testAlterYesToHalt():
for (progName, inString, solution) in [
('containsGAGA.py', 'GAGAGAGAG', 'halted'),
('containsGAGA.py', 'TTTTGGCCGGT', None),
]:
combinedString = utils.ESS(rf(progName), inString)
val = utils.runWithTimeout(None, alterYesToHalt, combinedString)
utils.tprint( (progName, inString), ":", val )
assert val == solution- The
alterYesToHaltprogram returns'halted'if \(P(I)=\)'yes'and otherwise enters an infinite loop using the utility functionutils.loop()function
YesOnString \(\leq_T\) HaltsOnString
yesViaHalts: uses thehaltsOnStringoracle to decideYesOnStringby calling the oracle on the transformed program.yesViaHaltsis functionally equivalent toYesOnString- However,
yesViaHaltsuseshaltsOnStringas a key building block
alterYesToHalt.py: transforms an instance(P, I)so that ifP(I)returns"yes"the transformed program halts (returns), otherwise it enters an infinite loop.haltsOnString: oracle “wrapper” that simulates a program with timeout and returns"yes"iff the program halts within the timeout period.Key insights about this proof technique using Turing reductions:
- Not a “direct” proof by contradiction for
HaltsOnString’s uncomputability - Instead, we prove
YesOnString\(\leq_T\) (“reduces to”)HaltsOnString - This reduction means that
YesOnStringis no harder thanHaltsOnString
- Not a “direct” proof by contradiction for
Reduction proof strategy
Key takeaways for proofgrammers
Key concepts learned this week: - Turing reductions: Way to prove problems uncomputable
- Oracle methodology: Assume solution exists to build contradiction
- Proof by contradiction: Powerful technique for impossibility results
- Problem hierarchies: Organize computational problems by difficulty
- Realization: From
YesOnString, many problems are uncomputable!
Practical skills developed this week: - Program transformation: Modify programs to change their behavior
- Reduction construction: Build systematic arguments for hardness
- Mathematical reasoning: Formal logic for computational problems
Proofgrammers